Welcome
Mission
Many engineering systems involve multiple disciplines and require the coupled analysis of those systems to evaluate their overall performance. In addition, we must consider interdisciplinary trade-offs to design such systems. Multidisciplinary design optimization (MDO) aims to assist the design of coupled engineering systems through the use of numerical methods for the analysis and design optimization. For a review of MDO methods (called architectures), see this survey paper. An aircraft is a prime example of a multidisciplinary system, and it is no coincidence that aircraft design was one of the very first applications of MDO. Prof. Martins founded the MDO Laboratory research group in 2002. The vision of our research group is that MDO will enable a relatively small team of engineers to explore possible designs quickly and early in the design process using powerful numerical tools.
Research
Research in the MDO Lab embraces both the theory and applications perspectives. On the theory side, we develop numerical methods that are applicable to a wide range of problems. Much of our work has focused on the accurate and efficient computation of derivatives to aid gradient-based optimization methods, but derivatives have many other applications. We have been collaborating with NASA in the development of OpenMDAO, a framework to facilitate the application of MDO to real world engineering design problems.
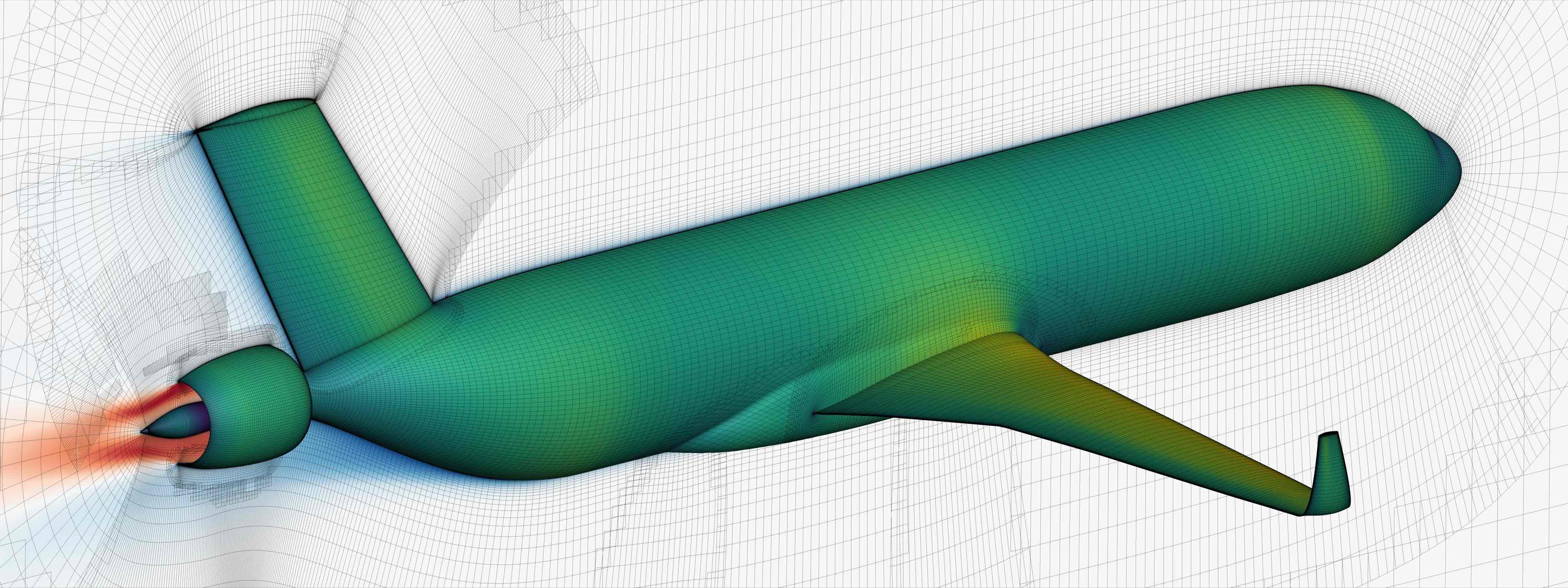
On the applications side, our focus has been on the optimization of aircraft configurations with the objective of minimizing environmental impact. Much of our effort has been in researching methods to enable high-fidelity aerostructural optimization, which optimizes aerodynamic shape and structural sizing simultaneously, leading to the optimal aeroelastic tailoring of wings. This led to the development of the framework for MDO of aircraft configurations with high fidelity (MACH). Using this framework, we have found wing shapes that minimize takeoff weight and fuel burn for a given mission, as well as configurations that minimize the aggregate fuel burn for thousands of missions. We have also considered the optimization of composite laminates and compared optimal metallic wings with composite ones. Another potential of application of aerostructural optimization is in the design of wind turbines.
Keeping up to date
To keep up to date with our latest publications, workshops, and open source software you can:
- Subscribe to our e-mail updates by sending a blank e-mail to engopt-join@mdolab.engin.umich.edu. (You can also unsubscribe at any time by e-mailing engopt-leave@mdolab.engin.umich.edu.)
- Follow us on the MDO Lab LinkdedIn page
- Follow Prof. Martins on ResearchGate